西瓜书中涉及的机器学习算法

这是笔者在准备nju推免机试时准备的自用资料，但是估计从今年（2025）过后不会再有这类型的机器学习算法题目了，可以作为学习西瓜书的一些参考（应该有不少谬误及typo）

---

常见损失函数

1. Mean Squared Error (MSE)

均方误差 (MSE) 用于回归任务，衡量预测值与真实值之间的平均平方差。

数学公式：

$$L_{\text{MSE}} = \frac{1}{N} \sum_{i=1}^{N} (y_{\text{true}}^i - y_{\text{pred}}^i)^2$$

• $y_{\text{true}}^i $是第 ( i ) 个样本的真实值。
• $ y_{\text{pred}}^i$ 是第 ( i ) 个样本的预测值。
• ( N ) 是样本总数。

2. Mean Absolute Error (MAE)

平均绝对误差 (MAE) 用于回归任务，衡量预测值与真实值之间的平均绝对差。

数学公式：

$$L_{\text{MAE}} = \frac{1}{N} \sum_{i=1}^{N} |y_{\text{true}}^i - y_{\text{pred}}^i|$$

• $ y_{\text{true}}^i $ 是第 ( i ) 个样本的真实值。
• $ y_{\text{pred}}^i $ 是第 ( i ) 个样本的预测值。

---

3. Binary Cross-Entropy

二分类交叉熵用于二分类任务，衡量模型预测的概率与真实标签之间的差异。

数学公式：

$$L_{\text{binary}} = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_{\text{true}}^i \log(y_{\text{pred}}^i) + (1 - y_{\text{true}}^i) \log(1 - y_{\text{pred}}^i) \right]$$

• ( $y_{\text{true}}^i \in \{0, 1\}$ ) 是第 ( i ) 个样本的真实标签。
• ( $y_{\text{pred}}^i $) 是第 ( i ) 个样本的预测概率。

---

4. Categorical Cross-Entropy

多分类交叉熵用于多分类任务，衡量模型预测的概率分布与真实标签的分布之间的差异。

数学公式：

$$L_{\text{categorical}} = - \frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{\text{true},c}^i \log(y_{\text{pred},c}^i)$$

• ( $y_{\text{true},c}^i \in \{0, 1\}$ ) 是第 ( i ) 个样本的真实标签的 one-hot 编码。
• ( $y_{\text{pred},c}^i $) 是第 ( i ) 个样本属于类别 ( c ) 的预测概率。
• ( C ) 是类别的总数。

---

5. Hinge Loss (SVM Loss)

铰链损失（SVM损失）通常用于支持向量机（SVM），它最大化分类边界。

数学公式：

$$L_{\text{hinge}} = \frac{1}{N} \sum_{i=1}^{N} \max(0, 1 - y_{\text{true}}^i y_{\text{pred}}^i)$$

• ( $y_{\text{true}}^i$ ) 是第 ( i ) 个样本的真实标签（取值为 ±1)）。
• ( $y_{\text{pred}}^i $) 是第 ( i ) 个样本的预测值。

---

6. Huber Loss

Huber 损失对回归任务中的异常值进行了处理，当误差较小时使用平方误差，误差较大时使用线性误差。

数学公式：

$$L_{\text{huber}} = \frac{1}{N} \sum_{i=1}^{N} \left[ \begin{array}{ll} 0.5 \cdot \left| y_{\text{true}}^i - y_{\text{pred}}^i \right|^2 & \text{if } \left| y_{\text{true}}^i - y_{\text{pred}}^i \right| \leq \delta \\ \delta \cdot \left( \left| y_{\text{true}}^i - y_{\text{pred}}^i \right| - 0.5 \cdot \delta \right) & \text{if } \left| y_{\text{true}}^i - y_{\text{pred}}^i \right| > \delta \end{array} \right.$$

• ( \delta ) 是一个超参数，控制“平滑”与“惩罚”之间的平衡。
• ( y_{\text{true}}^i ) 是第 ( i ) 个样本的真实值。
• ( y_{\text{pred}}^i ) 是第 ( i ) 个样本的预测值。

---

7. L2 Regularization Loss

L2 正则化损失常用于防止过拟合，鼓励模型参数的平方和较小。

数学公式：

$$L_{\text{L2}} = \lambda_{\text{reg}} \sum_{j=1}^{M} w_j^2$$

• ( w_j ) 是模型参数的第 ( j ) 个权重。
• ( \lambda_{\text{reg}} ) 是正则化系数。
• ( M ) 是参数的数量。
• • 惩罚的是参数的平方，所以对大的参数惩罚非常重（比如 w=10，惩罚是100；w=2，惩罚是4）。
  • 它会让所有参数都向0收缩，但通常不会让任何参数精确为0。
  • 结果是：所有特征都保留，但权重变小了，模型更平滑。
  • 处理特征相关性强

---

8. L1 Regularization Loss

L1 正则化损失常用于促进稀疏性，鼓励模型参数为零。

数学公式：

$$L_{\text{L1}} = \lambda_{\text{reg}} \sum_{j=1}^{M} |w_j|$$

• ( w_j ) 是模型参数的第 ( j ) 个权重。
• ( \lambda_{\text{reg}} ) 是正则化系数。
• ( M ) 是参数的数量。
• • 惩罚的是参数的绝对值，对大参数和小参数的惩罚是线性的。
  • 由于其几何特性（L1的等高线是菱形），优化过程中更容易“撞到角点”，而角点对应某些参数为0。
  • 结果是：会把不重要的特征的权重直接压缩为0，实现特征选择
  • 促进参数权重的稀疏性

---

9. Kullback-Leibler Divergence (KL Divergence)

KL 散度衡量两个概率分布之间的差异，常用于概率模型和生成模型。

数学公式：

$$D_{\text{KL}}(p || q) = \sum_{i=1}^{N} p_i \log \left( \frac{p_i}{q_i} \right)$$

• ( p_i ) 是真实分布的第 ( i ) 个概率值。
• ( q_i ) 是预测分布的第 ( i ) 个概率值。

---

10. Softmax Function

Softmax 函数将一个向量转换为概率分布，广泛应用于多分类问题。

数学公式：

$$\text{softmax}(x)_i = \frac{e^{x_i}}{\sum_{j=1}^{C} e^{x_j}}$$

• ( x_i ) 是输入向量 ( x ) 中的第 ( i ) 个元素。
• ( C ) 是类别的总数。

---

11. Softmax Loss

Softmax 损失（与交叉熵损失类似）常用于多分类问题中，结合 Softmax 函数计算损失。

数学公式：

$$L_{\text{softmax}} = - \frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{\text{true},c}^i \log(y_{\text{pred},c}^i)$$

• ( $y_{\text{true},c}^i \in \{0, 1\} $) 是第 ( i ) 个样本的真实标签的 one-hot 编码。
• ( $y_{\text{pred},c}^i $) 是第 ( i ) 个样本属于类别 ( c ) 的预测概率。

---

import numpy as np

# 1. Mean Squared Error (MSE)
def mean_squared_error(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 2. Mean Absolute Error (MAE)
def mean_absolute_error(y_true, y_pred):
    return np.mean(np.abs(y_true - y_pred))

# 3. Binary Cross-Entropy
def binary_crossentropy(y_true, y_pred):
    epsilon = 1e-15  # Avoid log(0)
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)  # Prevent y_pred from being 0 or 1
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))


//把 y_pred 的所有值限制在 [epsilon, 1 - epsilon] 范围内

# 4. Categorical Cross-Entropy
def categorical_crossentropy(y_true, y_pred):
    #numpy.clip(a, a_min, a_max, out=None)
    epsilon = 1e-15  # 避免对数计算时出现log(0)
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)  # 防止y_pred为0或1
    #y_true 必须是 one-hot 编码（独热编码） 的形式
    return -np.mean(np.sum(y_true * np.log(y_pred), axis=1))
    #axis=1出来时竖着，=0出来时横着

# 5. Hinge Loss (SVM Loss)
def hinge_loss(y_true, y_pred):
    return np.mean(np.maximum(0, 1 - y_true * y_pred))

# 6. Huber Loss
def huber_loss(y_true, y_pred, delta=1.0):
    error = np.abs(y_true - y_pred)
    is_small_error = error <= delta
    small_error_loss = 0.5 * error**2
    large_error_loss = delta * (error - 0.5 * delta)
    return np.mean(np.where(is_small_error, small_error_loss, large_error_loss))

# 7. L2 Regularization Loss
def l2_regularization_loss(weights, lambda_reg=0.01):
    return lambda_reg * np.sum(weights**2)

# 8. L1 Regularization Loss
def l1_regularization_loss(weights, lambda_reg=0.01):
    return lambda_reg * np.sum(np.abs(weights))

# 9. Kullback-Leibler Divergence (KL Divergence)
def kl_divergence(p, q):
    epsilon = 1e-15  # Prevent log(0)
    p = np.clip(p, epsilon, 1 - epsilon)
    q = np.clip(q, epsilon, 1 - epsilon)
    return np.sum(p * np.log(p / q))

# 10. Softmax Function
def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))  # Prevent overflow
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

# 11. Softmax Loss
def softmax_loss(y_true, y_pred):
    epsilon = 1e-15
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)  # Prevent log(0)
    return -np.mean(np.sum(y_true * np.log(y_pred), axis=1))

数据预处理

缺失值

如果数据中存在缺失值，可以选择填充它们，通常用均值或中位数来填充数值型数据。如果是类别数据，也可以选择填充众数。

mean_value = np.nanmean(column)#忽略nan值

column[np.isnan(column)] = mean_value # 填充nan缺失值为mean_value

import numpy as np

def fill_missing_values(data):
    '''
    使用每列的均值填充缺失值
    :param data: 数据集，类型为ndarray
    :return: 填充后的数据集
    '''
    # 遍历每一列，填充缺失值
    for i in range(data.shape[1]):
        column = data[:, i]
        # 计算列的均值（忽略nan）
        mean_value = np.nanmean(column)
        # 填充缺失值
        column[np.isnan(column)] = mean_value
    return data

标准化

对特征进行标准化，使其均值为0，方差为1，避免特征尺度对模型产生不良影响。标准化可以使用 (x - mean) / std 的方式来实现。

means=np.mean(data,axis=0) #取每一个特征的均值

std=np.std(data,axis=0) #取每一个特征的标准差

def standardize_data(data):
    '''
    标准化数据：每个特征减去均值，再除以标准差
    :param data: 数据集，类型为ndarray
    :return: 标准化后的数据集
    '''
    # 计算每列的均值和标准差
    means = np.mean(data, axis=0)
    stds = np.std(data, axis=0)

    # 标准化每一列
    standardized_data = (data - means) / stds
    return standardized_data

正则化

min_vals = np.min(data, axis=0)
max_vals = np.max(data, axis=0)

def normalize_data(data):
    '''
    归一化数据：将每个特征缩放到[0, 1]范围内
    :param data: 数据集，类型为ndarray
    :return: 归一化后的数据集
    '''
    # 计算每列的最小值和最大值
    min_vals = np.min(data, axis=0)
    max_vals = np.max(data, axis=0)

    # 归一化每一列
    normalized_data = (data - min_vals) / (max_vals - min_vals)
    return normalized_data

Z-score

可以使用 Z-Score 方法来去除异常值。通常认为 Z-Score 大于 3 或小于 -3 的样本是异常值。

filtered_data = data[np.all(np.abs(z_scores) < threshold, axis=1)]

• axis=1：沿着列方向判断（即：对每个样本的所有特征判断）
• np.all：要求所有特征都满足条件（即：所有特征的 |Z| < threshold）

def remove_outliers(data, threshold=3):
    '''
    使用 Z-Score 去除异常值
    :param data: 数据集，类型为ndarray
    :param threshold: Z-Score 阈值，默认是3
    :return: 去除异常值后的数据集
    '''
    # 计算每列的均值和标准差
    means = np.mean(data, axis=0)
    stds = np.std(data, axis=0)

    # 计算 Z-Score
    z_scores = (data - means) / stds

    # 过滤 Z-Score 小于阈值的数据
    filtered_data = data[np.all(np.abs(z_scores) < threshold, axis=1)]

    return filtered_data

import numpy as np
def linear_regression_gradient_descent(X: np.ndarray, y: np.ndarray, alpha: float, iterations: int) -> np.ndarray:
    # Your code here, make sure to round
    m,n=X.shape
    theta=np.zeros((n,1))
    y = y.reshape(-1, 1)  # (m,) -> (m, 1)
    for i in range(iterations):
        # 计算预测误差
        error = X @ theta - y  # (m, 1)
        # 计算梯度: (1/m) * X^T @ error
        gradient = (1/m) * X.T @ error
        # 更新参数
        theta -= alpha * gradient
    return np.round(theta,4)

Python 尝试广播 (3,1) 和 (3,)，但广播规则不匹配，y reshape 成 (m, 1)

广义线性模型

线性回归

MSE(mean squard error) MAE(mean absolute error) RMSE(root mse) R^2(R-squard)

np.mean((y_predict - y_test) ** 2) #mean自带了求和功能

X = np.hstack((np.ones((train_data.shape[0], 1)), train_data))#hstack添加一个偏置项b，每个样本的bias特征值为1

np.linalg.inv(X.T.dot(X)).dot(X.T).dot(train_label)

numpy.var(array, axis) #var为方差variance，std为标准差

numpy.vstack(([1,2,3],[4,5,6])) 行顺序堆叠

import numpy as np

# MSE
def mse_score(y_predict, y_test):
    return np.mean((y_predict - y_test) ** 2)

# R2
def r2_score(y_predict, y_test):
    '''
    input: y_predict (ndarray): 预测值
           y_test (ndarray): 真实值
    output: r2 (float): r2值
    '''
    t1 = np.sum((y_predict - y_test) ** 2)
    t2 = np.sum((y_test - np.mean(y_test)) ** 2)
    return 1 - t1 / t2

class LinearRegression:
    def __init__(self):
        '''初始化线性回归模型'''
        self.theta = None

    def fit_normal(self, train_data, train_label):
        '''
        input: train_data (ndarray): 训练样本
               train_label (ndarray): 训练标签
        '''
        X = np.hstack((np.ones((train_data.shape[0], 1)), train_data))
        #创建一个列向量，全为1，长度等于样本数
        self.theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(train_label)
        return self.theta

    def predict(self, test_data):
        '''
        input: test_data (ndarray): 测试样本
        '''
        test_data = np.hstack((np.ones((test_data.shape[0], 1)), test_data))
        return test_data.dot(self.theta)

逻辑回归Logistic Regression

逻辑回归是通过回归的思想来解决二分类问题的算法，用一个S型的函数（Sigmoid函数），把线性回归的结果压缩到 [0,1] 区间，解释为“属于某个类别的概率”。它内部还是在做线性回归 wTx+b，只是最后加了一个非线性变换（Sigmoid），用来做分类概率输出。可以使用np.exp(-z)

交叉熵损失yi代表真实类别，log(yi_hat)代表预测类别

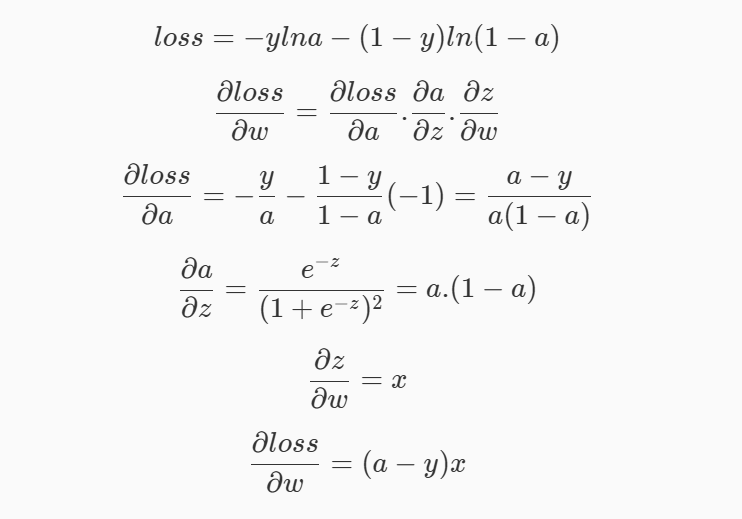
梯度下降

沿着“当前点的负梯度方向”走一小步，就能慢慢靠近最小值，在多维空间中，梯度向量是函数增长最快的方向。

大学习率收敛快，迅速接近最优解，但是容易震荡无法收敛，小学习率稳定收敛到精确解（可能局部），但是慢

问题	过拟合	欠拟合
表现	训练误差低，测试误差高	训练误差和测试误差都高，模型过于简单或不充分学习数据特征
学习率过大	可能导致模型无法稳定收敛，训练过程震荡，导致最终过拟合训练数据	过大的学习率可能跳过局部最优，导致无法捕捉到数据中的复杂模式，出现欠拟合
学习率过小	可能导致训练过程过于缓慢，使得模型误学习训练数据中的噪声，过拟合	过小的学习率可能导致参数更新不足，学习不到数据的复杂模式，造成欠拟合
解决方法	增加正则化，减少模型复杂度，更多数据，适当调整学习率	增加模型复杂度，训练更多轮次，使用合适的学习率

# -*- coding: utf-8 -*-

import numpy as np
import warnings
warnings.filterwarnings("ignore")

def sigmoid(x):
    '''
    sigmoid函数
    :param x: 转换前的输入
    :return: 转换后的概率
    '''
    return 1/(1+np.exp(-x))


def fit(x,y,eta=1e-3,n_iters=10000):
    '''
    训练逻辑回归模型
    :param x: 训练集特征数据，类型为ndarray
    :param y: 训练集标签，类型为ndarray
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :return: 模型参数，类型为ndarray
    '''
    #   请在此添加实现代码   #
    #********** Begin *********#
    m,n=x.shape
    theta=np.zeros(n)
    for i in range(n_iters):
        yy=x.dot(theta)
        z=sigmoid(yy)
        grad=x.T.dot(z-y)
        theta-=eta*grad
    return theta
    #********** End **********#

from sklearn.linear_model import LogisticRegression

def digit_predict(train_image, train_label, test_image):
    '''
    实现功能：训练模型并输出预测结果
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray,shape为[-1, 8, 8]
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''

    #************* Begin ************#
    train=train_image.reshape(len(train_image),-1)
#-1 表示自动计算维度，将除样本数量以外的维度全部拉平成一维。
    test=test_image.reshape(len(test_image),-1)
    model=LogisticRegression(max_iter=1000,C=12)
# C：正则化系数的倒数，默认为 1.0 ，越小代表正则化越强；
    model.fit(train,train_label)
    result=model.predict(test)
    return result
    #************* End **************#

感知机

它是一个二分类线性模型，核心思想是：找到一个超平面，将两类数据线性分开。

• 适用于线性可分数据集：即存在一个超平面能将两类样本完全分开。

• 不能处理非线性问题：如异或问题（XOR）感知机无法解决。

predict = np.where(output > 0, 1, -1)

predict=np.sign(output)

#encoding=utf8
import numpy as np
#构建感知机算法
class Perceptron(object):
    def __init__(self, learning_rate = 0.01, max_iter = 200):
        self.lr=learning_rate
        self.max_iter=max_iter
    def fit(self, data, label):
        '''
        input:data(ndarray):训练数据特征
              label(ndarray):训练数据标签
        output:w(ndarray):训练好的权重
               b(ndarry):训练好的偏置
        '''
        #编写感知机训练方法，w为权重，b为偏置

        #********* Begin *********#
        self.w=np.random.randn(data.shape[1])
        self.b=0
        for i in range(self.max_iter):
            for j in range(len(data)):
                output=self.w.dot(data[j].T)+self.b
                predict=1 if output>0 else -1
                if(label[j]*output<=0):
                    self.w+=self.lr*label[j]*data[j]
                    self.b+=self.lr*label[j]


        #********* End *********#
    def predict(self, data):
        '''
        input:data(ndarray):测试数据特征
        output:predict(ndarray):预测标签
        '''
        #********* Begin *********#
        output = np.dot(data, self.w) + self.b
        predict = np.where(output > 0, 1, -1)
        predict=np.sign(output)
        #********* End *********#
        return predict

#encoding=utf8
import os
import pandas as pd
from sklearn.linear_model.perceptron import Perceptron

if os.path.exists('./step2/result.csv'):
    os.remove('./step2/result.csv')

#********* Begin *********#
train_data=pd.read_csv('./step2/train_data.csv')
train_label=pd.read_csv('./step2/train_label.csv')
train_label=train_label['target']

test_data=pd.read_csv('./step2/test_data.csv')

model=Perceptron(eta0=0.1,max_iter=500)
#eta0：学习率大小，默认为 1.0 ；
#max_iter：最大训练轮数。
model.fit(train_data,train_label)
prediction=model.predict(test_data)
res=pd.DataFrame(prediction,columns=['result'])
res.to_csv('./step2/result.csv',index=False)
#********* End *********#

LDA（线性判别分析）

LDA 是一种 有监督降维 技术，其目标是将数据投影到一个低维空间中，使得不同类别之间尽可能可分。目标是最大化类间散度（类之间的距离），最小化类内散度（每类自己的分散程度）。

x0m = np.mean(x0, axis=0) # 类别 0 的均值向量,求样本的每个特征均值要加axis=0

sigma0 = np.cov(x0, rowvar=False)#默认 np.cov 会按行计算特征（即样本是列），但我们通常每一行是一个样本，所以需要加.T或使用rowvar=False

mean_diff = (x0m - x1m).reshape(-1, 1) # 列向量化, shape=(n,) 变成 shape=(n, 1)，列向量

return np.linalg.inv(sw).dot(x0m - x1m)

x_new = model.fit_transform(x, y)

import numpy as np

def lda(X, y):
    '''
    线性判别分析（Linear Discriminant Analysis）

    参数:
        X(ndarray): 样本特征矩阵，形状为 (n_samples, n_features)
        y(ndarray): 样本标签向量，取值为 0 或 1（仅支持二分类）

    返回:
        w(ndarray): 最优投影方向向量，用于将高维数据投影到一维，实现类别分离
    '''

    # 将数据按类别分开（这里是二分类，分成类 0 和类 1）
    x0 = X[y == 0]  # 类别 0 的所有样本
    x1 = X[y == 1]  # 类别 1 的所有样本

    # 分别计算每一类的均值向量（每个特征的均值）
    x0m = np.mean(x0, axis=0)  # 类别 0 的均值向量
    x1m = np.mean(x1, axis=0)  # 类别 1 的均值向量

    # 分别计算每一类的类内协方差矩阵（每一类内部的样本方差+协方差）
    # rowvar=False 表示按列计算协方差（列是特征，行是样本）

    sigma0 = np.cov(x0, rowvar=False)
    sigma1 = np.cov(x1, rowvar=False)

    # 总类内散度矩阵 Sw（两个类别的协方差矩阵之和）
    sw = sigma0 + sigma1

    # 类间散度矩阵 Sb = (μ1 - μ0)(μ1 - μ0)^T，衡量类别中心的分离程度
    mean_diff = (x0m - x1m).reshape(-1, 1)  # 列向量化
    sb = mean_diff @ mean_diff.T  # 外积构成类间散度矩阵

    # 计算广义特征值问题 Sw^-1 * Sb 的特征值与特征向量
    eigvals, eigvecs = np.linalg.eig(np.linalg.inv(sw).dot(sb))

    # 将特征值按从大到小排序，找出最大特征值对应的方向
    idx = np.argsort(eigvals)[::-1]  # 逆序排列索引
    w = eigvecs[:, idx[0]]  # 最大特征值对应的特征向量（最佳投影方向）

    return w  # 返回用于降维的最优方向向量

#encoding=utf8 
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

def lda(x,y):
    '''
    input:x(ndarray):待处理数据
          y(ndarray):待处理数据标签
    output:x_new(ndarray):降维后数据
    '''
    model = LinearDiscriminantAnalysis(n_components=2) 
    x_new = model.fit_transform(x, y)
    return x_new

多分类策略

OvO

将 K 类的多分类问题拆分为 $\frac{K(K-1)}{2}$ 个二分类问题，每个分类器只区分两个类别。

对于任意两个类别 $c_i$ 与 $c_j$（$i < j$）：

1. 从数据集中仅选出这两个类别的样本。

2. 用二分类模型训练出分类器 $f_{i,j}$，判断样本属于 $c_i$ 还是 $c_j$。

3. 最终得到 $\frac{K(K-1)}{2}$ 个分类器。

4. • 对测试样本 $x$，输入所有分类器 $f_{i,j}$。

   • 每个分类器对样本进行投票（即判断更像哪个类别）。

   • 汇总投票，得票最多的类别为最终预测类别。

self.classes_ = np.unique(y)

self.models[(cls1, cls2)] = model map

votes = [defaultdict(int) for _ in range(len(X))]

for (cls1, cls2), model in self.models.items()

`enumerate(preds) 的作用是：在遍历预测结果 preds 的同时，提供每个预测结果的索引。它返回的是 (索引, 值) 对。`

from collections import defaultdict
from sklearn.linear_model import LogisticRegression

class OvOClassifier:
    def __init__(self, base_model=None):
        self.base_model = base_model if base_model else LogisticRegression()
        self.models = {}
        self.classes_ = None

    def fit(self, X, y):
        self.classes_ = np.unique(y)
        self.models = {}

        for i in range(len(self.classes_)):
            for j in range(i + 1, len(self.classes_)):
                cls1, cls2 = self.classes_[i], self.classes_[j]
# 找到所有属于 cls1 或 cls2 的样本
X_pair = []
y_binary = []
for xi, yi in zip(X, y):
    if yi == cls1 or yi == cls2:
        X_pair.append(xi)
        y_binary.append(1 if yi == cls1 else 0)

X_pair = np.array(X_pair)
y_binary = np.array(


                model = LogisticRegression()
                model.fit(X_pair, y_binary)
                self.models[(cls1, cls2)] = model
#是一个 字典，key 是一个类别对的 元组，value 是对应的 训练好的模型对象

    def predict(self, X):
        votes = [defaultdict(int) for _ in range(len(X))]
#创建了一个列表 votes，这个列表有 len(X) 个元素，每个元素是一个 defaultdict(int)

        for (cls1, cls2), model in self.models.items():
            preds = model.predict(X)
            for i, pred in enumerate(preds):
                voted_class = cls1 if pred == 1 else cls2
                votes[i][voted_class] += 1

        final_preds = []
        final_preds = [max(vote, key=vote.get) for vote in votes]

#vote 是一个 dict（通常是像 {'A': 2, 'B': 3} 这样的结构），键是类别，值是票数；

#vote.get 用作 key 函数，表示对每个键使用 vote.get(键) 作为排序依据；

#max(...) 找出拥有最多票数的类别。

        return np.array(final_preds)

OvR

将一个 K 类的多分类问题拆解为 K 个二分类问题。每个分类器的任务是识别某一个类别（“正类”）与其余所有类别（“负类”）之间的区别。

假设标签集合为 $C = {c_1, c_2, …, c_K}$

对于每一个类别 $c_i$：

1. 创建一个新的二分类训练集：

   • 样本属于 $c_i$ 的，标签为 1（正类）

   • 样本不属于 $c_i$ 的，标签为 0（负类）

2. 用一个二分类器（如 Logistic Regression、SVM）训练该数据子集。

3. 共训练 K 个分类器，分别记为 $f_1, f_2, …, f_K$。

4. • 对于一个测试样本 $x$，将其输入所有分类器 $f_1(x), …, f_K(x)$。

   • 每个分类器输出一个置信度/得分。

   • 选择得分最高的那个分类器所代表的类别作为预测结果。

特性	OvR (One-vs-Rest)	OvO (One-vs-One)
分类器数量	K	K(K-1)/2
每个分类器训练样本	全部样本（正类 vs 其他）	两类样本
预测机制	最大置信度	多数投票
实现复杂度	较低	较高
优点	简洁、高效	更适合类别数少、边界复杂的任务
缺点	易受类别不均衡影响	分类器数量多、计算成本高

import numpy as np

# 逻辑回归类
class tiny_logistic_regression(object):
    def __init__(self):
        # W 是系数，b 是截距
        self.coef_ = None
        self.intercept_ = None
        self._theta = None  # 存储所有的 W 和 b
        self.label_map = {}  # 0/1 到标签的映射

    def _sigmoid(self, x):
        return 1. / (1. + np.exp(-x))  # Sigmoid 激活函数

    # 训练模型
    def fit(self, train_datas, train_labels, learning_rate=1e-4, n_iters=1e3):
        # 计算损失函数
        def J(theta, X_b, y):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
            except:
                return float('inf')  # 避免计算出错

        # 损失函数对 theta 的梯度
        def dJ(theta, X_b, y):
            return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)

        # 批量梯度下降
        def gradient_descent(X_b, y, initial_theta, learning_rate, n_iters=1e2, epsilon=1e-6):
            theta = initial_theta
            cur_iter = 0
            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - learning_rate * gradient  # 更新 theta
                # 判断是否满足收敛条件
                if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
                    break
                cur_iter += 1
            return theta

        # 将训练数据加上截距项（x0 = 1）
        X_b = np.hstack([np.ones((len(train_datas), 1)), train_datas])
        initial_theta = np.zeros(X_b.shape[1])  # 初始化theta为零
        self._theta = gradient_descent(X_b, train_labels, initial_theta, learning_rate, n_iters)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    # 预测样本属于正类的概率
    def predict_proba(self, X):
        X_b = np.hstack([np.ones((len(X), 1)), X])
        return self._sigmoid(X_b.dot(self._theta))

    # 预测：如果属于正类的概率 >= 0.5，则预测为1，否则为0
    def predict(self, X):
        proba = self.predict_proba(X)
        return np.array(proba >= 0.5, dtype='int')

# One-vs-Rest (OvR) 分类器
class OvR(object):
    def __init__(self):
        self.models = []  # 用于保存每个类别的二分类器
        self.real_label = []  # 用于保存正类标签

    def fit(self, train_datas, train_labels):
        '''
        OvR的训练阶段，将模型保存到self.models中
        :param train_datas: 训练集数据，类型为ndarray
        :param train_labels: 训练集标签，类型为ndarray，shape为(-1,)
        :return: None
        '''
        self.classes = np.unique(train_labels)  # 获取所有类别标签

        for cls in self.classes:
            # 将当前类别作为正类，其他类别作为负类
            y_binary = (train_labels == cls).astype(int)
            model = tiny_logistic_regression()
            model.fit(train_datas, y_binary)  # 使用二分类器训练模型
            self.models.append(model)  # 将训练好的模型加入模型列表
            self.real_label.append(cls)  # 保存当前类别的标签

    def predict(self, test_datas):
        '''
        OvR的预测阶段
        :param test_datas: 测试集数据，类型为ndarray
        :return: 预测结果，类型为ndarray
        '''
        # 存储每个样本对每个类别的概率
        all_probs = np.zeros((len(test_datas), len(self.classes)))

        for i, model in enumerate(self.models):
            # 获取每个模型对每个测试样本属于该类别的概率
            probs = model.predict_proba(test_datas)
            all_probs[:, i] = probs  # 存储该类别的概率

        # 每个样本选择概率最大的类别
        predicted_class_indices = np.argmax(all_probs, axis=1)
        return self.real_label[predicted_class_indices]  # 返回每个样本的最终预测类别

决策树

信息增益

np.log2,Counter,len,np.unique

for label,count in labelcount.items():

import numpy as np
from collections import Counter

def calcInfoGain(feature, label, index):
    '''
    计算信息增益
    :param feature: 测试用例中的特征矩阵，类型为ndarray
    :param label: 测试用例中的标签，类型为ndarray
    :param index: 特征列的索引，指示使用第几个特征来计算信息增益。
    :return: 信息增益，类型float
    '''

    # 计算原始熵
    all_count = len(label)

    # 获取标签的频率
    label_count = Counter(label)

    # 计算标签的熵
    all_entropy = 0
    for label_value, count in label_count.items():
        p = count / all_count
        all_entropy -= p * np.log2(p)

    # 计算按特征划分后的熵
    feature_values = np.unique(feature[:, index])  # 获取该特征的所有可能值
# feature[:, index] 表示选择 feature 矩阵的所有行（: 表示所有行），但是只选择第 index 列（即该列所有样本的特征值）。
    weighted_entropy = 0

    for value in feature_values:
        # 根据特征值划分数据
        subset_label = label[feature[:, index] == value]
        subset_count = len(subset_label)

        # 计算子集的熵
        subset_entropy = 0
        subset_label_count = Counter(subset_label)
        for subset_label_value, count in subset_label_count.items():
            p = count / subset_count
            subset_entropy -= p * np.log2(p)

        # 加权平均子集的熵
        weighted_entropy += (subset_count / all_count) * subset_entropy

    # 信息增益 = 总熵 - 加权熵
    info_gain = all_entropy - weighted_entropy
    return info_gain return info_gain

信息增益率

def calcInfoGainRatio(feature, label, index):

    #********* Begin *********#

    all_count=len(label)

    #D

    needE=0

    all_features = np.unique(feature[:, index])  # 获取该特征列的所有唯一值

    for f in all_features:

        count=0

        for j in range(len(label)):

            if feature[j][index]==f:

                count+=1

        #D1

        needE-=(count/all_count)*np.log2(count/all_count)

    gain=calcInfoGain(feature,label,index)

    return gain/needE

    #********* End *********#

Gini系数

def calcGini(feature, label, index):
    '''
    '''
    #********* Begin *********#
    #先计算特征个数，在用特征里面的小个数计算
    allcount=len(label)
    feats=np.unique(feature[:,index])
    Gini=0
    for val in feats:
        sub_count=0
        sublabels=[]
        subG=1
        for j in range(allcount):
            if feature[j][index]==val:
                sub_count+=1
                sublabels.append(label[j])

        label_count=Counter(sublabels)
        for la,co in label_count.items():
            subG-=(co/sub_count)**2
        Gini+=subG*(sub_count/allcount)
    return Gini

    #********* End *********#

鸢尾花识别

pd.read_csv,to_csv,DataFrame,

import numpy as np
from sklearn.tree import DecisionTreeClassifier
import pandas as pd
#********* Begin *********#

model=DecisionTreeClassifier()
train_label = pd.read_csv('./step7/train_label.csv').values
train_data = pd.read_csv('./step7/train_data.csv').values
test_data = pd.read_csv('./step7/test_data.csv').values


model.fit(train_data,train_label)
result=model.predict(test_data)
resultd=pd.DataFrame(result,columns=['prediction'])
resultd.to_csv('./step7/predict.csv',index=False)
#********* End *********#

贝叶斯分类器

全概率公式

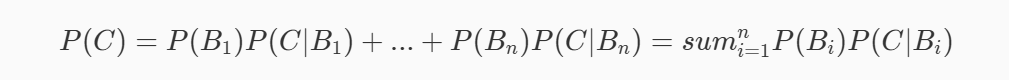
贝叶斯公式（条件概率乘法定理/全概率公式）

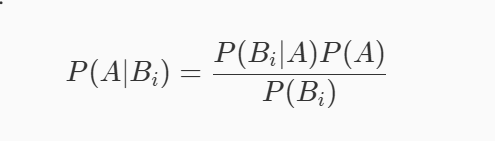
朴素贝叶斯分类

label_val, label_count = np.unique(label, return_counts=True)

self.label_prob = {label_val[i]: label_count[i] / all_count for i in range(len(label_val))}

feat_lines = feature[label == val]

for a, b in zip(feat_val, feat_count):

import numpy as np

class NaiveBayesClassifier(object):
    def __init__(self):
        self.label_prob = {}  # 每种类别在数据中出现的概率
        self.condition_prob = {}  # 条件概率 P(x|y)

    def fit(self, feature, label):
        '''
        对模型进行训练，计算各种概率
        :param feature: 训练数据集的特征，ndarray
        :param label: 训练数据集的标签，ndarray
        :return: 无返回
        '''
        # 计算每个标签的概率 P(y)
        label_val, label_count = np.unique(label, return_counts=True)
        all_count = len(label)
        self.label_prob = {label_val[i]: label_count[i] / all_count for i in range(len(label_val))}

        # 计算每个标签下特征的条件概率 P(x|y)
        feat_num = feature.shape[1]  # 特征数量
        self.condition_prob = {}

        for val in label_val:
            feat_lines = feature[label == val]  # 当前标签下的特征数据
            feature_prob = {}

            for i in range(feat_num):
                feat_val, feat_count = np.unique(feat_lines[:, i], return_counts=True)  # 当前特征列的取值及其频数
                feature_prob[i] = {}
                sub_count = len(feat_lines)
                for a, b in zip(feat_val, feat_count):
                    feature_prob[i][a] = b / sub_count  # 计算条件概率

            self.condition_prob[val] = feature_prob  # 保存当前标签的条件概率

    def predict(self, feature):
        '''
        对数据进行预测，返回预测结果
        :param feature: 测试数据集所有特征组成的ndarray
        :return: 预测的标签
        '''
        predictions = []

        for sample in feature:
            label_post = {}

            # 计算每个标签的后验概率 P(y|x)
            for label_val, prob in self.label_prob.items():
                probability = np.log2(prob)  # P(y)

                # 计算当前标签下的条件概率 P(x|y)
                for idx, val in enumerate(sample):
                    probability += np.log2(self.condition_prob[label_val][idx].get(val, 1e-10))

                label_post[label_val] = probability

            # 选择后验概率最大的标签作为预测结果
            predict = max(label_post, key=label_post.get)
            predictions.append(predict)

        return np.array(predictions)  # 返回 numpy 数组

Laplace平滑

假设N表示训练数据集总共有多少种类别，Ni表示训练数据集中第i列总共有多少种取值。则训练过程中在算类别的概率时分子加1，分母加N，算条件概率时分子加1，分母加Ni

import numpy as np

class NaiveBayesClassifier(object):
    def __init__(self):
        '''
        '''
        self.label_prob = {}  # 存储每个类别的先验概率
        self.condition_prob = {}  # 存储每个类别下每个特征的条件概率

    def fit(self, feature, label):
        '''
        对模型进行训练，计算每种类别的先验概率和条件概率
        :param feature: 训练数据集所有特征组成的 ndarray
        :param label: 训练数据集所有标签组成的 ndarray
        :return: 无返回值，通过更新 self.label_prob 和 self.condition_prob 来保存训练结果
        '''
        #********* Begin *********#
        row_num = len(feature)  # 样本的数量
        col_num = len(feature[0])  # 特征的数量
        unique_label_count = len(set(label))  # 唯一类别的数量

        # 计算每个类别的出现次数
        for c in label:
            if c in self.label_prob:
                self.label_prob[c] += 1
            else:
                self.label_prob[c] = 1

        # 计算每个类别的先验概率，并进行拉普拉斯平滑
        for key in self.label_prob.keys():
            self.label_prob[key] += 1  # 拉普拉斯平滑
            self.label_prob[key] /= (unique_label_count + row_num)  # 计算先验概率

            # 构建条件概率字典，初始化每个类别下每个特征值的概率
            self.condition_prob[key] = {}
            for i in range(col_num):
                self.condition_prob[key][i] = {}
                for k in np.unique(feature[:, i], axis=0):  # 遍历每个特征的不同取值
                    self.condition_prob[key][i][k] = 1  # 初始概率设为 1（拉普拉斯平滑）

        # 统计训练集中每个类别下特征值的频次
        for i in range(len(feature)):
            for j in range(len(feature[i])):
                # 更新每个特征值的出现频次
                self.condition_prob[label[i]][j][feature[i][j]] += 1

        # 计算每个类别下每个特征值的条件概率，进行拉普拉斯平滑
        for label_key in self.condition_prob.keys():
            for k in self.condition_prob[label_key].keys():
                total = len(self.condition_prob[label_key][k].keys())  # 特征的种类数
                for v in self.condition_prob[label_key][k].values():
                    total += v  # 总的计数值（包括平滑项）
                for kk in self.condition_prob[label_key][k].keys():
                    # 计算条件概率
                    self.condition_prob[label_key][k][kk] /= total
        #********* End *********#

    def predict(self, feature):
        '''
        对数据进行预测，返回预测结果
        :param feature: 测试数据集所有特征组成的 ndarray
        :return: 预测结果的数组，包含每个测试样本的预测类别
        '''
        result = []  # 存储预测结果
        # 对每条测试数据进行预测
        for i, f in enumerate(feature):
            prob = np.zeros(len(self.label_prob.keys()))  # 存储每个类别的概率，初始化为零
            ii = 0  # 用于索引类别
            for label, label_prob in self.label_prob.items():
                prob[ii] = label_prob  # 初始化为先验概率
                for j in range(len(f)):  # 遍历当前样本的所有特征
                    # 计算该特征值在该类别下的条件概率
                    prob[ii] *= self.condition_prob[label][j][f[j]]
                ii += 1  # 处理下一个类别
            # 选择具有最大概率的类别作为预测结果
            result.append(list(self.label_prob.keys())[np.argmax(prob)])
        return np.array(result)  # 返回预测结果

新闻文本分类

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import TfidfTransformer
import numpy as np

def news_predict(train_sample, train_label, test_sample):
    '''
    训练模型并进行预测，返回预测结果
    :param train_sample: 原始训练集中的新闻文本，类型为 ndarray
    :param train_label: 训练集中新闻文本对应的主题标签，类型为 ndarray
    :param test_sample: 原始测试集中的新闻文本，类型为 ndarray
    :return: 预测结果，类型为 ndarray
    '''
    #********* Begin *********#
    # 实例化CountVectorizer，转换文本为词频矩阵
    vec = CountVectorizer()
    X_train = vec.fit_transform(train_sample)  # 先fit拟合训练集，再对训练集进行词频向量化
    X_test = vec.transform(test_sample)  # 对测试集进行词频向量化

    # 实例化TfidfTransformer，转换为TF-IDF矩阵
    tfidf = TfidfTransformer()
    X_train = tfidf.fit_transform(X_train)  # 将训练集词频矩阵转换为TF-IDF矩阵
    X_test = tfidf.transform(X_test)  # 将测试集词频矩阵转换为TF-IDF矩阵

    # 实例化MultinomialNB模型，设置平滑参数alpha=0.8
    model = MultinomialNB(alpha=0.8)
    model.fit(X_train, train_label)  # 使用训练集训练模型

    # 预测测试集的标签
    result = model.predict(X_test)

    # 返回预测结果
    return np.array(result)
    #********* End *********#

支持向量机

线性SVM

计算训练数据的均值和标准差 mean = np.mean(train_data, axis=0) std = np.std(train_data,axis=0)

train_data = (train_data - mean) / std

model = LinearSVC(C=10, max_iter=10000) # 增大C的值并增加最大迭代次数

C（正则化参数）: 控制模型的复杂度，较大的 C 值会让模型更加“严格”地拟合训练数据，但可能导致过拟合。较小的 C 值则允许更多的错误，从而使得模型更为平滑，防止过拟合

#encoding=utf8
from sklearn.svm import LinearSVC
import pandas as pd
import numpy as np

def linearsvc_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    # ********* Begin *********#

    # 1. 数据标准化（手动进行标准化：均值0，方差1）
    # 计算训练数据的均值和标准差
    mean = np.mean(train_data, axis=0)
    std = np.std(train_data, axis=0)

    # 对训练数据和测试数据进行标准化
    train_data = (train_data - mean) / std
    test_data = (test_data - mean) / std

    # 2. 创建并训练模型
    model = LinearSVC(C=10, max_iter=10000)  # 增大C的值并增加最大迭代次数
    model.fit(train_data, train_label)

    # 3. 预测测试数据
    predict = model.predict(test_data)

    # ********* End *********# 
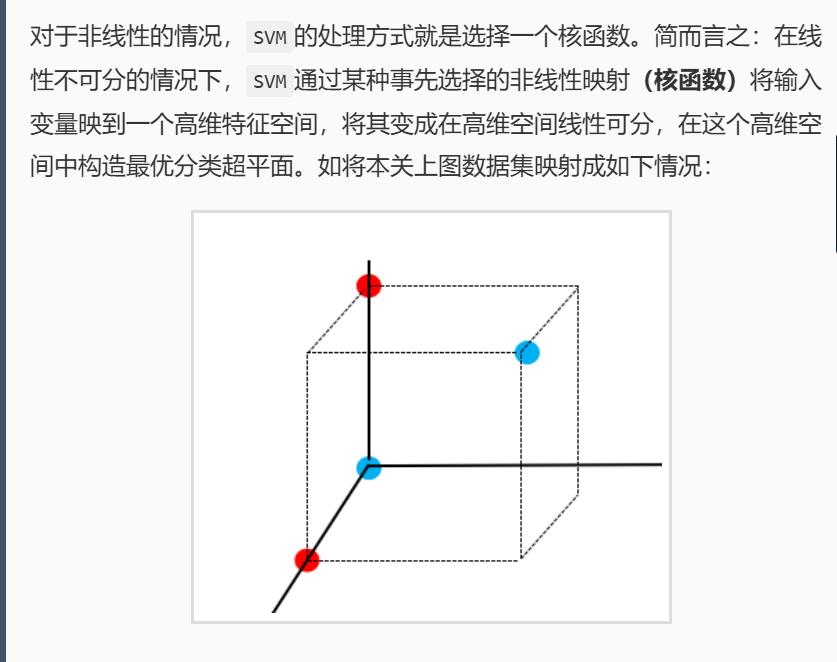
    return predict

非线性SVM

#encoding=utf8
from sklearn.svm import SVC

def svc_predict(train_data,train_label,test_data,kernel):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
          kernel(str):使用核函数类型:
              'linear':线性核函数
              'poly':多项式核函数
              'rbf':径像核函数/高斯核
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********# 
    model=SVC(kernel=kernel)
    model.fit(train_data,train_label)
    predict=model.predict(test_data)
    #********* End *********# 
    return predict

集成学习

boosting

提升方法基于这样一种思想：对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好。

历史上，Kearns 和 Valiant 首先提出了强可学习和弱可学习的概念指出：在 PAC 学习的框架中，一个概念，

如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；

一个概念，如果存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。

非常有趣的是 Schapire 后来证明强可学习与弱可学习是等价的，也就是说，在 PAC 学习的框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。

这样一来，问题便成为，在学习中，如果已经发现了弱学习算法，那么能否将它提升为强学习算法。大家知道，发现弱学习算法通常要比发现强学习算法容易得多。那么如何具体实施提升，便成为开发提升方法时所要解决的问题。

与 bagging 不同， boosting 采用的是一个串行训练的方法。首先，它训练出一个弱分类器，然后在此基础上，再训练出一个稍好点的弱分类器，以此类推，不断的训练出多个弱分类器，最终再将这些分类器相结合，这就是 boosting 的基本思想

可以看出，子模型之间存在强依赖关系，必须串行生成。 boosting 是利用不同模型的相加，构成一个更好的模型，求取模型一般都采用序列化方法，后面的模型依据前面的模型

Adaboost算法原理
对提升方法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值或概率分布；二是如何将弱分类器组合成一个强分类器

关于第 1 个问题，AdaBoost的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值

这样一来，那些没有得到正确分类的数据，由于其权值的加大而受到后一轮的弱分类器的更大关注。于是，分类问题被一系列的弱分类器“分而治之”。

至于第 2 个问题，即弱分类器的组合，AdaBoost采取加权多数表决的方法，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用。

bagging

与 Boosting 这种串行集成学习算法不同， Bagging 是并行式集成学习方法。

如果使用 Bagging 解决分类问题，就是将多个分类器的结果整合起来进行投票，选取票数最高的结果作为最终结果。如果使用 Bagging 解决回归问题，就将多个回归器的结果加起来然后求平均，将平均值作为最终结果。

n足够大时，考虑用正态分布来拟合二项分布

Bagging 在训练时的特点就是随机有放回采样和并行。

随机有放回采样: 假设训练数据集有 m 条样本数据，每次从这 m 条数据中随机取一条数据放入采样集，然后将其返回，让下一次采样有机会仍然能被采样。然后重复 m 次，就能得到拥有 m 条数据的采样集，该采样集作为 Bagging 的众多分类器中的一个作为训练数据集。假设有 T 个分类器（随便什么分类器），那么就重复 T 此随机有放回采样，构建出 T 个采样集分别作为 T 个分类器的训练数据集。

并行： 假设有 10 个分类器，在 Boosting 中，1 号分类器训练完成之后才能开始 2 号分类器的训练，而在 Bagging 中，分类器可以同时进行训练，当所有分类器训练完成之后，整个 Bagging 的训练过程就结束了。

samples = np.random.choice(n, n, replace=True)从0到n-1选取n个有放回采样，

prediction=[model.predict(feature) for model in self.models]

votes=[prediction[j][i] for j in range(self.n_model)]

max(set(votes),key=votes.count)以votes.count为排序依据，对set(votes)进行排序并取最大值

import numpy as np
from sklearn.tree import DecisionTreeClassifier

class BaggingClassifier():
    def __init__(self, n_model=10):
        '''
        初始化函数，设置模型参数
        :param n_model: 分类器数量，默认为10个决策树
        '''
        # 分类器的数量，默认为10
        self.n_model = n_model
        # 用于保存训练后的模型，存储每个决策树
        self.models = []

    def fit(self, feature, label):
        # 获取样本数量
        n = len(label)

        # 训练 n_model 个决策树
        for i in range(self.n_model):
            # 有放回地随机采样样本索引
            samples = np.random.choice(n, n, replace=True)

            # 生成样本的特征和标签子集
            sample_f = feature[samples]
            sample_l = label[samples]

            # 使用决策树模型进行训练，最大深度为3
            model = DecisionTreeClassifier(max_depth=3)
            model.fit(sample_f, sample_l)

            # 将训练好的模型添加到模型列表中
            self.models.append(model)

    def predict(self, feature):
        '''
        对测试集数据进行预测，采用投票机制
        :param feature: 测试集数据，类型为ndarray，形状为 (n_samples, n_features)
        :return: 预测结果，类型为ndarray，形状为 (n_samples,)
        '''
        # 存储每个模型的预测结果

        prediction=[]
        for model in self.models:
            prediction.append(model.predict(feature))
        # prediction=[model.predict(feature) for model in self.models]
        final_prediction=[]
        for i in range(len(feature)):
            votes=[prediction[j][i] for j in range(self.n_model)]
            l=max(set(votes),key=votes.count)
            final_prediction.append(l)

        return np.array(final_prediction)

        #************* End **************#

随机森林

随机森林是 Bagging 的一种扩展变体，随机森林的训练过程相对与 Bagging 的训练过程的改变有：

基学习器： Bagging 的基学习器可以是任意学习器，而随机森林则是以决策树作为基学习器。
随机属性选择： 假设原始训练数据集有 10 个特征，从这 10 个特征中随机选取 k 个特征构成训练数据子集，然后将这个子集作为训练集扔给决策树去训练。其中 k 的取值一般为 log2(特征数量) 。
这样的改动通常会使得随机森林具有更加强的泛化性，因为每一棵决策树的训练数据集是随机的，而且训练数据集中的特征也是随机抽取的。如果每一棵决策树模型的差异比较大，那么就很容易能够解决决策树容易过拟合的问题。

随机森林的预测流程与 Bagging 的预测流程基本一致，如果是回归，就将结果基学习器的预测结果全部加起来算平均；如果是分类，就投票，票数最多的结果作为最终结果。但需要注意的是，在预测时所用到的特征必须与训练模型时所用到的特征保持一致。

s = np.random.choice(l, self.feature_nums, replace=False)随机选择不重复的特征

sub_sample = sample_f[:, s]在s列的所有行数据

votes.append(model.predict([sub_f])[0]) # 获取预测结果

import numpy as np
from collections import Counter
from sklearn.tree import DecisionTreeClassifier

class RandomForestClassifier():
    def __init__(self, n_model=10):
        '''
        初始化函数
        '''
        self.n_model = n_model
        self.feature_nums = None
        self.models = []
        self.col_indexs = []

    def fit(self, feature, label):
        '''
        训练模型
        :param feature: 训练集数据，类型为ndarray
        :param label: 训练集标签，类型为ndarray
        :return: None
        '''
        n, l = feature.shape
        if self.feature_nums is None:
            self.feature_nums = int(np.log2(l))  # 取整以确保feature_nums是整数

        for i in range(self.n_model):
            # 有放回采样
            sample = np.random.choice(n, n, replace=True)
            sample_f = feature[sample]
            sample_l = label[sample]

            # 随机选择特征列
            s = np.random.choice(l, self.feature_nums, replace=False)
            self.col_indexs.append(s)

            sub_sample = sample_f[:, s]
            model = DecisionTreeClassifier(max_depth=3)
            model.fit(sub_sample, sample_l)
            self.models.append(model)

    def predict(self, feature):
        '''
        :param feature: 测试集数据，类型为ndarray
        :return: 预测结果，类型为ndarray
        '''
        predictions = []   
        for j in range(feature.shape[0]):  # 遍历每个测试样本
            votes = []
            for i, model in enumerate(self.models):  # 遍历每棵决策树
                col = self.col_indexs[i]  # 获取模型训练时使用的特征列
                sub_f = feature[j, col]  # 获取测试样本的特征
                votes.append(model.predict([sub_f])[0])  # 获取预测结果

            # 投票机制，选择出现次数最多的结果
            predictions.append(max(set(votes), key=votes.count))

        return np.array(predictions)

聚类

层次聚类距离计算：

dist = np.linalg.norm(i - j) #直接计算i，j的欧氏距离

return np.min(dist) #np.argmin(dist)返回索引

import numpy as np

def calc_min_dist(cluster1, cluster2):
    '''
    计算簇间最小距离
    :param cluster1:簇1中的样本数据，类型为ndarray
    :param cluster2:簇2中的样本数据，类型为ndarray
    :return:簇1与簇2之间的最小距离
    '''
    min_dist = float('inf')  # 初始化最小距离为正无穷大
    for i in cluster1:
        for j in cluster2:
            dist = np.linalg.norm(i - j)  # 计算欧几里得距离
            if dist < min_dist:
                min_dist = dist
    return min_dist


def calc_max_dist(cluster1, cluster2):
    '''
    计算簇间最大距离
    :param cluster1:簇1中的样本数据，类型为ndarray
    :param cluster2:簇2中的样本数据，类型为ndarray
    :return:簇1与簇2之间的最大距离
    '''
    max_dist = -float('inf')  # 初始化最大距离为负无穷大
    for i in cluster1:
        for j in cluster2:
            dist = np.linalg.norm(i - j)  # 计算欧几里得距离
            if dist > max_dist:
                max_dist = dist
    return max_dist


def calc_avg_dist(cluster1, cluster2):
    '''
    计算簇间平均距离
    :param cluster1:簇1中的样本数据，类型为ndarray
    :param cluster2:簇2中的样本数据，类型为ndarray
    :return:簇1与簇2之间的平均距离
    '''
    total_dist = 0
    count1 = 0
    count2 = 0
    for i in cluster1:
        for j in cluster2:
            total_dist += np.linalg.norm(i - j)  # 计算欧几里得距离

    return total_dist / (len(cluster1)*len(cluster2))  # 返回平均距离

k-means

距离度量

曼哈顿距离即每个维度距离求和，欧氏距离即空间直线距离

def distance(x,y,p=2):
    '''
    input:x(ndarray):第一个样本的坐标
          y(ndarray):第二个样本的坐标
          p(int):等于1时为曼哈顿距离，等于2时为欧氏距离
    output:distance(float):x到y的距离      
    ''' 
    if(p==1):
          return sum(np.abs(x-y))
    else:
          return np.sqrt(sum((x-y)**2))

质心计算

dist=np.power(np.sum(np.abs(x-y)**p),1/p)

Cmass=np.mean(data,axis=0);

dist_list=sorted(dist)

#encoding=utf8
import numpy as np
#计算样本间距离
def distance(x, y, p=2):

    #********* Begin *********#
    # 计算x和y之间差的绝对值的p次方  
    dist=np.power(np.sum(np.abs(x-y)**p),1/p)
    # 计算最终的距离值 
    #********* End *********#
    return dist

#计算质心
def cal_Cmass(data):
    '''
    input:data(ndarray):数据样本
    output:mass(ndarray):数据样本质心
    '''
    #********* Begin *********#
    # 计算数据样本的质心（即每个维度的平均值）  
    Cmass=np.mean(data,axis=0)
    #********* End *********#
    return Cmass

#计算每个样本到质心的距离，并按照从小到大的顺序排列
def sorted_list(data,Cmass):
    '''
    input:data(ndarray):数据样本
          Cmass(ndarray):数据样本质心
    output:dis_list(list):排好序的样本到质心距离
    '''
    #********* Begin *********#
    # 初始化一个空列表，用于存储距离  
    dist=[]
    # 遍历数据样本中的每个样本 
    for sample in data:
        dis=distance(Cmass,sample)
        dist.append(dis)
    # 计算当前样本到质心的距离，并添加到列表中  
    # 对距离列表进行排序  
    dist_list=sorted(dist)
    return dist_list
    #********* End *********#

k-means

model = KMeans(n_clusters=k, init='k-means++', max_iter=500, tol=1e-4, random_state=42)

K-means 是一种 无监督学习 方法，它确实没有使用真实标签（ground truth labels），但仍然会为每个样本分配一个 聚类标签（cluster index），这个标签是算法自动生成的，表示样本属于哪个簇（cluster）

1. 初始化聚类中心

   • 随机选择 k 个样本作为初始聚类中心 centroids。

2. 迭代优化（直到收敛或达到最大迭代次数）：

   • 步骤 1：分配样本到最近的簇

     • 对每个样本 x ∈ X，计算它与所有 centroids 的距离，并分配到最近的簇。

     • 代码实现：create_clusters(centroids, X)。

   • 步骤 2：更新聚类中心

     • 对每个簇，计算其所有样本的均值，作为新的聚类中心。

     • 代码实现：update_centroids(clusters)。

   • 步骤 3：检查收敛

     • 如果新旧聚类中心的距离变化 <= ε（varepsilon），则停止迭代。

     • 否则，继续迭代。

3. 返回聚类标签

   • 最终，为每个样本分配其最近的聚类中心的索引，作为聚类标签 labels。

labels = np.zeros(X.shape[0], dtype=int)

return np.argmin(distance)

clusters=[[] for _ in range(self.k)]

new_centroids[i] = np.mean(clusters[i], axis=0)

centroid_shift = np.linalg.norm(new_centroids - centroids)

#NumPy 提供的一个线性代数函数，用来计算矩阵的“范数”，在这里是计算 向量的欧几里得距离

sample=np.random.choice(len(X),self.k,replace=False)

#encoding=utf8
import numpy as np

# 计算一个样本与数据集中所有样本的欧氏距离的平方
def euclidean_distance(one_sample, X):
    return np.sum((X - one_sample) ** 2, axis=1)


class Kmeans():
    """Kmeans聚类算法.
    Parameters:
    -----------
    k: int
        聚类的数目.
    max_iterations: int
        最大迭代次数. 
    varepsilon: float
        判断是否收敛, 如果上一次的所有k个聚类中心与本次的所有k个聚类中心的差都小于varepsilon, 
        则说明算法已经收敛
    """
    def __init__(self, k=2, max_iterations=500, varepsilon=0.0001):
        self.k = k
        self.max_iterations = max_iterations
        self.varepsilon = varepsilon
        np.random.seed(1)
    #********* Begin *********#
    # 从所有样本中随机选取self.k样本作为初始的聚类中心
    def init_random_centroids(self, X):
        sample=np.random.choice(len(X),self.k,replace=False)
        return X[sample]

    # 返回距离该样本最近的一个中心索引[0, self.k)
    def _closest_centroid(self, sample, centroids):
        distance=euclidean_distance(sample,centroids)
        return np.argmin(distance)


    # 将所有样本进行归类，归类规则就是将该样本归类到与其最近的中心
    def create_clusters(self, centroids, X):
        clusters=[[] for _ in range(self.k)]
        for sample in X:
            closest_idx=self._closest_centroid(sample,centroids)
            clusters[closest_idx].append(sample)
        return clusters


    # 对中心进行更新
    def update_centroids(self, clusters, X):
        new_centroids = np.zeros((self.k, len(clusters[0][0])))
        for i in range(self.k):
            # 对每个簇内样本求均值
            new_centroids[i] = np.mean(clusters[i], axis=0)
        return new_centroids


    # 对整个数据集X进行Kmeans聚类，返回其聚类的标签
    def predict(self, X):
        # 从所有样本中随机选取self.k样本作为初始的聚类中心
        centroids=self.init_random_centroids(X)
        # 迭代，直到算法收敛(上一次的聚类中心和这一次的聚类中心几乎重合)或者达到最大迭代次数   
        for i in range(self.max_iterations):
            clusters=self.create_clusters(centroids,X)
            new_centroids=self.update_centroids(clusters,X)

            centroid_shift = np.linalg.norm(new_centroids - centroids)
            if centroid_shift <= self.varepsilon:
                break
            # 更新聚类中心
            centroids = new_centroids
            # 如果聚类中心几乎没有变化，说明算法已经收敛，退出迭代
        labels = np.zeros(X.shape[0], dtype=int)
        for i, sample in enumerate(X):
            labels[i] = self._closest_centroid(sample, centroids)
        return labels

DBSCAN

• 簇（Cluster） = 高密度区域（数据点密集）。

• 噪声（Noise） = 低密度区域（数据点稀疏）。

• eps (ε)：邻域半径，用于判断两个点是否“相邻”。

• min_samples：形成一个簇所需的最小样本数（核心点的邻域至少要有这么多点）。

类型	定义	示例
核心点（Core Point）	在 eps 邻域内至少有 min_samples 个点（包括自己）	若 min_samples=5，某点周围有 ≥5 个点（含自己），则它是核心点
边界点（Border Point）	在某个核心点的 eps 邻域内，但自身不满足核心点条件	周围点 < min_samples，但属于某个核心点的邻域
噪声点（Noise Point）	既不是核心点，也不是边界点	离群点，不属于任何簇

• 如果点 q 在点 p 的 eps 邻域内，且 p 是核心点，则称 q 从 p 密度直达。

• 如果存在一个核心点序列 p1, p2, ..., pn，使得 pi+1 从 pi 密度直达，则称 p1 和 pn 密度相连。

1. 随机选择一个未访问的点 p。

2. 检查 p 的 eps 邻域：

   • 如果 p 是核心点（邻域内点数 ≥ min_samples）：

     • 创建一个新簇。

     • 递归地找出所有从 p 密度可达的点，加入该簇。

   • 如果 p 是噪声点，标记为噪声。

3. 重复上述过程，直到所有点被访问。

• 不需要预先指定簇数量（k）（比 K-means 更灵活）。

• 能发现任意形状的簇（K-means 只能发现球形簇）。

• 能识别噪声点（适合处理离群值）。

• 对参数 eps 和 min_samples 敏感，需要调参。

  | 特性 | DBSCAN | K-means |
  | —————— | ——————————- | ———- |
  | 簇形状 | 任意形状 | 球形 |
  | 噪声处理 | 能识别噪声 | 不能 |
  | 需指定簇数（k） | 不需要 | 需要 |
  | 参数依赖 | eps 和 min_samples | k |
  | 适合场景 | 非凸簇、噪声多 | 凸簇、数据均匀 |

  neighbors += new_neighbors # 将新邻域的点加入待处理列表
fit_predict() 是一个结合了训练和预测的简化语法，通常在 聚类 或 无监督学习 中使用，它的作用是：首先对数据进行训练（拟合模型），然后直接对数据进行预测，返回聚类标签或者分类标签。这种方法可以简化代码并提高效率，尤其是在进行无监督学习时

#encoding=utf8 
import numpy as np
import random

# 寻找eps邻域内的点
def findNeighbor(j, X, eps):
    """
    计算样本X[j]的eps邻域，返回所有在该邻域内的点的索引

    input:
        j (int): 当前点的索引
        X (ndarray): 样本数据
        eps (float): 邻域半径
    output:
        N (list): 邻域内的点的索引
    """
    N = []  # 存放邻域内的点
    for p in range(X.shape[0]):  # 遍历所有点
        # 计算欧式距离
        temp = np.sqrt(np.sum(np.square(X[j] - X[p])))  
        if temp <= eps:  # 如果点p在eps半径范围内
            N.append(p)  # 将该点加入邻域列表
    return N

def expandCluster(X, labels, point, neighbors, cluster_id, eps, min_Pts):
    """
    扩展簇，将密度可达的点加入到当前簇

    input:
        X (ndarray): 样本数据
        labels (list): 当前的聚类标签
        point (int): 当前扩展的核心点的索引
        neighbors (list): 核心点的邻域
        cluster_id (int): 当前簇的ID
        eps (float): 邻域半径
        min_Pts (int): 最小邻域内点数
    """
    labels[point] = cluster_id  # 将当前点标记为当前簇的成员
    i = 0
    while i < len(neighbors):  # 遍历邻域中的每一个点
        neighbor_point = neighbors[i]
        # 如果邻居点是噪声（未分类），将其标记为当前簇的一部分
        if labels[neighbor_point] == -1:  
            labels[neighbor_point] = cluster_id
        # 如果邻居点没有被标记，且它是一个核心点，则继续扩展簇
        elif labels[neighbor_point] == 0:
            labels[neighbor_point] = cluster_id
            new_neighbors = findNeighbor(neighbor_point, X, eps)
            if len(new_neighbors) >= min_Pts:  # 如果该点是核心点
                neighbors += new_neighbors  # 将新邻域的点加入待处理列表
        i += 1

# DBSCAN算法
def dbscan(X, eps, min_Pts):
    '''
    输入:
        X (ndarray): 样本数据
        eps (float): eps邻域半径
        min_Pts (int): eps邻域内最少点个数
    输出:
        labels (list): 聚类结果，每个点的标签（-1表示噪声，其他数字表示簇编号）
    '''
    # 样本数量
    nums = len(X)
    labels = np.zeros(nums)  # 初始化所有点的标签为0（表示未处理）
    cluster_id = 0  # 聚类编号初始化为0

    # 遍历每个样本点
    for i in range(nums):
        if labels[i] != 0:  # 如果该点已经被处理过，跳过
            continue
        else:
            # 获取点i的邻域
            neighbors = findNeighbor(i, X, eps)

            if len(neighbors) < min_Pts:  # 如果邻域内的点数小于min_Pts，标记为噪声
                labels[i] = -1
            else:  # 如果是核心点，则扩展簇
                cluster_id += 1  # 创建一个新的簇
                labels[i] = cluster_id  # 将当前点标记为该簇
                expandCluster(X, labels, i, neighbors, cluster_id, eps, min_Pts)

    return labels  # 返回聚类结果

AGNES

自底向上的不断合并簇直到簇数量满足要求

clusters[cova] += clusters[covb] 合并簇

del clusters[covb] # 删除第二个簇

import numpy as np

def AGNES(feature, k):
    '''
    AGNES聚类并返回聚类结果，量化距离时请使用簇间最大欧氏距离
    假设数据集为`[1, 2], [10, 11], [1, 3]]，那么聚类结果可能为`[[1, 2], [1, 3]], [[10, 11]]]
    :param feature:数据集，类型为ndarray
    :param k:表示想要将数据聚成`k`类，类型为`int`
    :return:聚类结果，类型为list
    '''
    #********* Begin *********#
    clusters=[[feature[i]] for i in range(len(feature))]
    cluster_nums=len(clusters)
    while cluster_nums > k:
        dist_min = 1e9
        cova, covb = -1, -1

        # 寻找距离最小的簇对
        for idx1 in range(cluster_nums):
            for idx2 in range(idx1 + 1, cluster_nums):
                # 计算两个簇之间的最小欧氏距离
                dist = []
                for i in clusters[idx1]:
                    for j in clusters[idx2]:
                        dist.append(np.linalg.norm(i - j))
                curr_max = np.min(dist)  # 选择最小欧氏距离

                if curr_min < dist_min:
                    dist_min = curr_max
                    cova, covb = idx1, idx2

        # 合并最小距离的两个簇
        clusters[cova] += clusters[covb]
        del clusters[covb]  # 删除第二个簇

        # 更新簇的数量
        cluster_nums -= 1
    #********* End *********#

EM算法

单次迭代

np.sum(np.abs(np.array(new_thetas)-np.array(thetas))

import numpy as np

def em_single(init_values, observations):
    pa, pb = init_values
    a_heads = 0
    a_tails = 0
    b_heads = 0
    b_tails = 0

    for trial in observations:
        num_heads = sum(trial)
        num_tails = len(trial) - num_heads

        log_ka = np.sum([np.log(pa if coin == 1 else 1 - pa) for coin in trial])
        log_kb = np.sum([np.log(pb if coin == 1 else 1 - pb) for coin in trial])

        # Convert log-probabilities to probabilities safely
        max_log = max(log_ka, log_kb)
        exp_ka = np.exp(log_ka - max_log)
        exp_kb = np.exp(log_kb - max_log)
        total = exp_ka + exp_kb
        softa = exp_ka / total
        softb = exp_kb / total

        a_heads += softa * num_heads
        a_tails += softa * num_tails
        b_heads += softb * num_heads
        b_tails += softb * num_tails

    return [a_heads / (a_heads + a_tails), b_heads / (b_heads + b_tails)]

def em(observations, thetas, tol=1e-4, iterations=100):
    """
    模拟抛掷硬币实验并使用EM算法估计硬币A与硬币B正面朝上的概率。
    :param observations: 抛掷硬币的实验结果记录，类型为list。
    :param thetas: 硬币A与硬币B正面朝上的概率的初始值，类型为list，如[0.2, 0.7]代表硬币A正面朝上的概率为0.2，硬币B正面朝上的概率为0.7。
    :param tol: 差异容忍度，即当EM算法估计出来的参数theta不怎么变化时，可以提前挑出循环。例如容忍度为1e-4，则表示若这次迭代的估计结果与上一次迭代的估计结果之间的L1距离小于1e-4则跳出循环。为了正确的评测，请不要修改该值。
    :param iterations: EM算法的最大迭代次数。为了正确的评测，请不要修改该值。
    :return: 将估计出来的硬币A和硬币B正面朝上的概率组成list或者ndarray返回。如[0.4, 0.6]表示你认为硬币A正面朝上的概率为0.4，硬币B正面朝上的概率为0.6。
    """

    #********* Begin *********#
    new_thetas=0
    for i in range(iterations):
        new_thetas=em_single(thetas,observations)
        if(np.sum(np.abs(np.array(new_thetas)-np.array(thetas)))<tol):
            break
        thetas=new_thetas

    return new_thetas

    #********* End *********#

性能指标

外部指标

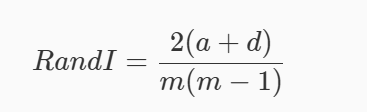
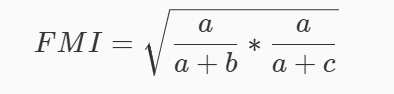
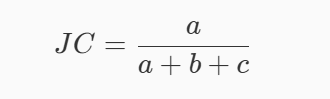
if y_true[i] == y_true[j] and y_pred[i] == y_pre #求与操作用and，&是位运算

a+=1

def calc(y_true, y_pred):
    a = b = c = d = 0
    for i in range(len(y_true)):
        for j in range(i + 1, len(y_pred)):
            if y_true[i] == y_true[j] and y_pred[i] == y_pred[j]:
                a += 1
            elif y_true[i] == y_true[j] and y_pred[i] != y_pred[j]:
                b += 1
            elif y_true[i] != y_true[j] and y_pred[i] == y_pred[j]:
                c += 1
            else:
                d += 1
    return [a, b, c, d]

def calc_JC(y_true, y_pred):
    ex = calc(y_true, y_pred)
    return ex[0] / (ex[0] + ex[1] + ex[2]) if (ex[0] + ex[1] + ex[2]) != 0 else 0.0

def calc_FM(y_true, y_pred):
    ex = calc(y_true, y_pred)
    if (ex[0] + ex[1]) == 0 or (ex[0] + ex[2]) == 0:
        return 0.0
    return np.sqrt((ex[0] / (ex[0] + ex[1])) * (ex[0] / (ex[0] + ex[2])))

def calc_Rand(y_true, y_pred):
    m = len(y_true)
    ex = calc(y_true, y_pred)
    return 2 * (ex[0] + ex[3]) / (m * (m - 1)) if m > 1 else 0.0

内部指标

DB 指数越小就越就意味着簇内距离越小同时簇间距离越大，也就是说DB 指数越小越好

Dunn 指数越大意味着簇内距离越小同时簇间距离越大，也就是说 Dunn 指数 越大越好

np.array,arr.tolist

import numpy as np
a = [1, 2, 3]
arr = np.array(a)

arr = np.array([1, 2, 3])
a = arr.tolist()

centroids = np.array([np.mean(feature[pred == label], axis=0) for label in labels])

import numpy as np

def calc_DBI(feature, pred):
    labels = np.unique(pred)
    k = len(labels)
    centroids = np.array([np.mean(feature[pred == label], axis=0) for label in labels])

    # 计算每个簇的类内平均距离（紧密度）
    s = []
    for label in labels:
        cluster_points = feature[pred == label]
        centroid = np.mean(cluster_points, axis=0)
        distances = np.sqrt(np.sum((cluster_points - centroid) ** 2, axis=1))
        s.append(np.mean(distances))
    s = np.array(s)

    # 计算簇质心间的距离矩阵
    M = np.zeros((k, k))
    for i in range(k):
        for j in range(k):
            if i != j:
                M[i][j] = np.linalg.norm(centroids[i] - centroids[j])

    # DBI 计算
    dbi = 0
    for i in range(k):
        max_r = -np.inf
        for j in range(k):
            if i != j:
                r = (s[i] + s[j]) / M[i][j]
                if r > max_r:
                    max_r = r
        dbi += max_r
    return dbi / k


    for label in labels:
        feat=feature[pred==label]
        center=np.mean(feat,axis=0)
        dist=[]
        for i in feat:
            dist.append(np.linalg.norm(i-center))
        s.append(np.mean(dist))
    #s[i]为簇内平均距离
    maxsum=0
    for i in range(k):
        max1=0
        for j in range(k):
            if(i!=j):
                max1=max((s[i]+s[j])/np.linalg.norm(centroids[i]-centroids[j]),max1)
        maxsum+=max1
    return maxsum/k



    #********* End *********#


def calc_DI(feature, pred):
    labels = np.unique(pred)
    k = len(labels)

    # 计算每个簇的最大内部距离
    max_intra = 0
    for label in labels:
        points = feature[pred == label]
        for i in range(len(points)):
            for j in range(i + 1, len(points)):
                dist = np.linalg.norm(points[i] - points[j])
                if dist > max_intra:
                    max_intra = dist

    # 计算簇间最小距离
    min_inter = np.inf
    for i in range(k):
        for j in range(i + 1, k):
            points_i = feature[pred == labels[i]]
            points_j = feature[pred == labels[j]]
            for p in points_i:
                for q in points_j:
                    dist = np.linalg.norm(p - q)
                    if dist < min_inter:
                        min_inter = dist

    return min_inter / max_intra if max_intra != 0 else 0

降维

维数灾难通常是指对于已知样本数目，存在一个特征数目的最大值，当实际使用的特征数目超过这个最大值时，机器学习算法的性能不是得到改善，而是退化（过拟合）。

• 降低机器学习算法的时间复杂度；

• 节省了提取不必要特征的开销；

• 缓解因为维数灾难所造成的过拟合现象。

PCA主成分分析

PCA 是将数据从原来的坐标系转换到新的坐标系，新的坐标系的选择是由数据本身决定的。

第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且方差最大的方向。然后该过程一直重复，重复次数为原始数据中的特征数量。最后会发现大部分方差都包含在最前面几个新坐标轴中，因此可以忽略剩下的坐标轴，从而达到降维的目的。

PCA 在降维时，需要指定将维度降至多少维，假设降至 k 维，则 PCA 的算法流程如下：

demean；
计算数据的协方差矩阵；
计算协方差矩阵的特征值与特征向量；
按照特征值，将特征向量从大到小进行排序；
选取前 k 个特征向量作为转换矩阵；
demean 后的数据与转换矩阵做矩阵乘法获得降维后的数据

matrix=np.cov(data.T) #cov函数期望行代表特征

val, vec = np.linalg.eigh(mat) #计算特征值和特征向量

indices = np.argsort(val)[::-1] # 倒序排序，val越大越重要

vec_res = vec_sort[:,:k]

import numpy as np

def pca(data, k):
    '''
    对data进行PCA，并将结果返回
    :param data: 数据集，类型为ndarray
    :param k: 想要降成几维，类型为int
    :return: 降维后的数据，类型为ndarray
    '''

    #********* Begin *********#
    # 均值归一化
    me = np.mean(data, axis=0)
    data = data - me

    # 计算协方差矩阵    
    # after_demean的行数为样本个数，列数为特征个数
    # 由于cov函数的输入希望是行代表特征，列代表数据的矩阵，所以要转置
    mat = np.cov(data.T)

    # 计算特征值和特征向量
    val, vec = np.linalg.eigh(mat)

    # 按特征值从大到小排序，选择前k个特征向量
    indices = np.argsort(val)[::-1]  # 倒序排序，val越大越重要
    vec_sort = vec[:, indices]       # 按排序后的索引选择特征向量

    # 选择前k个主成分
    vec_res = vec_sort[:, [i for i in range(k)]]        # 取前k列

    # 返回降维后的数据
    return data.dot(vec_res)
    #********* End *********#

MDS多维缩放

MDS 算法认为，在数据样本中，每个样本的每个特征值并不是数据间关系的必要特征，真正的基础特征是每个点与数据集中其他点的距离。

H = np.eye(n_samples) - np.ones((n_samples, n_samples)) / n_samples #单位阵减去1/n全一矩阵

B = -0.5 * np.dot(H, np.dot(distance_matrix ** 2, H))

eigvals_k = np.diag(np.sqrt(eigvals_sorted[:k])) #取前 k 个排序好的特征值，先开平方，然后把它们放到一个对角矩阵中

import numpy as np

def euclidean_distance(x, y):
    """计算欧几里得距离"""
    return np.sqrt(np.sum((x - y) ** 2))

def compute_distance_matrix(data):
    """计算距离矩阵"""
    n_samples = data.shape[0]
    distance_matrix = np.zeros((n_samples, n_samples))
    for i in range(n_samples):
        for j in range(n_samples):
           distance_matrix[i, j] = euclidean_distance(data[i], data[j])
    return distance_matrix

def mds(data, k):
    """
    手动实现MDS降维
    :param data: 原始数据 (样本，特征) 形式的 numpy 数组
    :param k: 目标降维的维度，默认2
    :return: 降维后的数据
    """
    # 1. 计算距离矩阵
    distance_matrix = compute_distance_matrix(data)

    # 2. 中心化距离矩阵
    n_samples = distance_matrix.shape[0]
    H = np.eye(n_samples) - np.ones((n_samples, n_samples)) / n_samples
    B = -0.5 * np.dot(H, np.dot(distance_matrix ** 2, H))

    # 3. 特征值分解
    eigvals, eigvecs = np.linalg.eigh(B)

    # 4. 按照特征值从大到小排序
    sorted_indices = np.argsort(eigvals)[::-1]  # 降序排列
    eigvals_sorted = eigvals[sorted_indices]
    eigvecs_sorted = eigvecs[:, sorted_indices]

    # 5. 选择前k个特征值和特征向量
    eigvals_k = np.diag(np.sqrt(eigvals_sorted[:k]))
    eigvecs_k = eigvecs_sorted[:, :k]

    # 6. 计算低维坐标
    low_dim_data = np.dot(eigvecs_k, eigvals_k)

    return low_dim_data  # 返回转置后的低维数据



# -*- coding: utf-8 -*-
from sklearn.manifold import MDS

def mds(data,d):
    '''
    input:data(ndarray):待降维数据
          d(int):降维后数据维度
    output:Z(ndarray):降维后数据
    '''
    #********* Begin *********#
    model=MDS(n_components=d)
#n_components ：即我们进行 MDS 降维时降到的维数。在降维时需要输入这个参数。
    Z=model.fit_transform(data)

    #********* End *********#
    return Z

Isomap等度量映射

Isomap 算法可以看作是 “在局部保持邻居关系的基础上，再用 MDS 降维”

Z = V @ L #特征向量组成的矩阵在左边，乘特征值构成的的对角阵

model = Isomap(n_components=d,n_neighbors=k) 取k个相邻数据，降到d维

# -*- coding: utf-8 -*-
import numpy as np

def isomap(data, d, k, Max=1e9):
    '''
    input:
        data(ndarray): 待降维数据，shape=(n_samples, n_features)
        d(int): 降维后数据维数
        k(int): 最近的k个样本
        Max(float): 表示无穷大
    output:
        Z(ndarray): 降维后的数据，shape=(n_samples, d)
    '''
    n = data.shape[0]

    # Step 1: 计算欧氏距离矩阵
    dist_matrix = np.zeros((n, n))
    for i in range(n):
        for j in range(i + 1, n):
            dist = np.linalg.norm(data[i] - data[j])
            dist_matrix[i][j] = dist_matrix[j][i] = dist

    # Step 2: 构建 k-近邻图（非邻接的点设为 Max）
    graph = np.full((n, n), Max)
    for i in range(n):
        neighbors = np.argsort(dist_matrix[i])[1:k+1]  # 取前k个最近邻（排除自身）
        for j in neighbors:
            graph[i][j] = dist_matrix[i][j]
            graph[j][i] = dist_matrix[i][j]  # 保持对称

    # Step 3: 使用 Floyd-Warshall 算法求最短路径（近似测地线）
    for k_mid in range(n):
        for i in range(n):
            for j in range(n):
                if graph[i][j] > graph[i][k_mid] + graph[k_mid][j]:
                    graph[i][j] = graph[i][k_mid] + graph[k_mid][j]

    # Step 4: 多维尺度分析 (MDS)
    D = graph
    D_squared = D ** 2
    H = np.eye(n) - np.ones((n, n)) / n
    B = -0.5 * H @ D_squared @ H

    # Step 5: 特征值分解
    eigvals, eigvecs = np.linalg.eigh(B)
    idx = np.argsort(eigvals)[::-1]
    eigvals = eigvals[idx]
    eigvecs = eigvecs[:, idx]

    # Step 6: 计算嵌入坐标 Z
    L = np.diag(np.sqrt(eigvals[:d]))
    V = eigvecs[:, :d]
    Z = V @ L

    return Z


# -*- coding: utf-8 -*-
from sklearn.manifold import Isomap

def isomap(data,d,k):
    '''
    input:data(ndarray):待降维数据
          d(int):降维后数据维度
          k(int):最近的k个样本
    output:Z(ndarray):降维后数据
    '''
    #********* Begin *********#
    model = Isomap(n_components=d,n_neighbors=k)
    Z=model.fit_transform(data)

    #********* End *********#
    return Z

LLE局部线性嵌入

Z = data[N_i] - data[i] # shape: (k, m)

C = Z.dot(Z.T) # 计算邻居之间差异的协方差矩阵 C，形状是 (k, k)

C += np.eye(k) * 1e-3 # 为了数值稳定，给协方差矩阵 C 加上一个小的正则项（0.001）

w = np.linalg.solve(C, ones) # 解线性方程组，得到每个邻居的权重

W[i, N_i[j]] = w[j] # 将第 j 个邻居的权重填入相应位置

M = (I - W).T.dot(I - W) # 计算矩阵 M，形式为 (I - W)^T * (I - W)

Z = eigvecs[:, idx[1:d+1]] # 选取最小的 d 个特征值对应的特征向量（跳过第一个全1特征向量）

# encoding=utf8 
import numpy as np

# 计算数据集的欧氏距离矩阵
def calc_dist(data):
    n = data.shape[0]  # 获取样本数目
    dist_matrix = np.zeros((n, n))  # 初始化一个 n x n 的距离矩阵
    for i in range(n):
        for j in range(n):
            # 计算第 i 个样本与第 j 个样本的欧氏距离
            dist_matrix[i, j] = np.linalg.norm(data[i] - data[j])  # np.linalg.norm 计算欧氏距离
    return dist_matrix

# 找到每个样本的 k 个最近邻
def find_neighbors(dist_matrix, k):
    n = dist_matrix.shape[0]  # 获取样本数目
    neighbors = np.zeros((n, k), dtype=int)  # 初始化一个 n x k 的邻居矩阵
    for i in range(n):
        # 对于每个样本，按距离从小到大排序，找到前 k 个邻居（排除自己）
        sorted_indices = np.argsort(dist_matrix[i])  # 排序，返回排序后的索引
        neighbors[i] = sorted_indices[1:k+1]  # 排除自己（即第一个是自己，跳过）
    return neighbors

# 局部线性嵌入（LLE）算法
def lle(data, d, k):
    n, m = data.shape  # n: 样本数目, m: 原始特征维度
    dist_matrix = calc_dist(data)  # 计算数据点之间的距离矩阵
    neighbors = find_neighbors(dist_matrix, k)  # 找到每个样本的 k 个邻居

    # 初始化权重矩阵 W，存储每个样本到其邻居的权重
    W = np.zeros((n, n))

    # 对于每个样本，计算其到邻居的权重
    for i in range(n):
        # 获取第 i 个样本的 k 个邻居的索引
        N_i = neighbors[i]
        # 构建邻居矩阵 Z：每列是一个邻居与 x_i 的差
        Z = data[N_i] - data[i]  # Z 的形状是 (k, m)，即每行是一个邻居的差向量
        C = Z.dot(Z.T)  # 计算邻居之间差异的协方差矩阵 C，形状是 (k, k)
        C += np.eye(k) * 1e-3  # 为了数值稳定，给协方差矩阵 C 加上一个小的正则项（0.001）
#在计算协方差矩阵 C = Z.dot(Z.T) 时，可能会遇到矩阵 C 变得奇异（即行列式为零），特别是当邻居之间的差异非常小或者完全相同时。这种情况下，矩阵 C 可能不可逆，导致无法进行后续的线性求解。

        # 解线性方程 Cw = 1，得到权重 w
        ones = np.ones(k)  # 创建一个大小为 k 的全1向量
        w = np.linalg.solve(C, ones)  # 解线性方程组，得到每个邻居的权重
        w = w / np.sum(w)  # 归一化权重，使得它们的和为 1

        # 将计算得到的权重 w 填入第 i 行的权重矩阵 W 中
        for j in range(k):
            W[i, N_i[j]] = w[j]  # 将第 j 个邻居的权重填入相应位置

    # 构造矩阵 M = (I - W)^T * (I - W)
    I = np.eye(n)  # n x n 的单位矩阵
    M = (I - W).T.dot(I - W)  # 计算矩阵 M，形式为 (I - W)^T * (I - W)

    # 计算 M 的特征值和特征向量
    eigvals, eigvecs = np.linalg.eigh(M)  # eigvals: 特征值, eigvecs: 特征向量

    # 选择最小的 d+1 个特征值对应的特征向量（第一个特征值是 0 对应的全1向量，跳过）
    idx = np.argsort(eigvals)  # 获取特征值的排序索引
    Z = eigvecs[:, idx[1:d+1]]  # 选取最小的 d 个特征值对应的特征向量（跳过第一个全1特征向量）

    return Z  # 返回降维后的数据



# -*- coding: utf-8 -*-
from sklearn.manifold import LocallyLinearEmbedding

def lle(data,d,k):
    '''
    input:data(ndarray):待降维数据
          d(int):降维后数据维度
          k(int):邻域内样本数
    output:Z(ndarray):降维后数据
    '''
    #********* Begin *********#
    model=LocallyLinearEmbedding(n_components=d,n_neighbors=k)
    Z=model.fit_transform(data)

    #********* End *********#
    return Z